Results Reproducibility

Case study: Application to Austrian COVID-19 survey

We use the methodology developed in this paper for the case of the COVID-19 prevalence estimation using the results of a survey done in November 2020 by Statistics Austria (2020). We also compare the different approaches, in order to illustrate, in practice, the impact of choosing one method rather than another one. In November 2020, a survey sample of \(n=2287\) was collected to test for COVID-19 using PCR-tests. Seventy-two participants were tested positive, and among these ones, thirty-five (\(R_1=35\)) had declared to have been tested positive with the official procedure, during the same month. In November, there were \(93914\) declared cases among the official (approximately) \(7166167\) inhabitants in Austria (above 16 years old), so that \(\pi_0 \approx 1.3105\%\). The sensitivity (\(1-\alpha\)) and the specificity (\(1-\beta\)) are not known with precision, so that we present estimates of the prevalence without misclassification error as well as for values for the FP and FN rates, that are plausible given the data and according to the sensitivity and specificity reported in or .

The results presented in Table 2 of Guerrier, Kuzmics, and Victoria-Feser (2024) can be reproduced as follows:

# Load pempi
library(pempi)

# Austrian data (November 2020)
pi0 = 93914/7166167

# Load data
data("covid19_austria")

# Random sampling
n = nrow(covid19_austria)
R1 = sum(covid19_austria$Y == 1 & covid19_austria$Z == 1)
R2 = sum(covid19_austria$Y == 0 & covid19_austria$Z == 1)
R3 = sum(covid19_austria$Y == 1 & covid19_austria$Z == 0)
R4 = sum(covid19_austria$Y == 0 & covid19_austria$Z == 0)

# Weighted sampling
R1w = sum(covid19_austria$weights[covid19_austria$Y == 1 & covid19_austria$Z == 1])
R2w = sum(covid19_austria$weights[covid19_austria$Y == 0 & covid19_austria$Z == 1])
R3w = sum(covid19_austria$weights[covid19_austria$Y == 1 & covid19_austria$Z == 0])
R4w = sum(covid19_austria$weights[covid19_austria$Y == 0 & covid19_austria$Z == 0])

# Print table
data_mat = matrix(c(R1w, R2w, R3w, R4w, R1, R2, R3, R4), 2, 4, byrow = TRUE)
rownames(data_mat) = c("Weighted sampling", "Unweighted sampling")
colnames(data_mat) = c("R1 (R11)", "R2 (R10)", "R3 (R01)", "R4 (R00)")
knitr::kable(round(data_mat, 4))

	R1 (R11)	R2 (R10)	R3 (R01)	R4 (R00)
Weighted sampling	33.3589	0	38.2712	2218.37
Unweighted sampling	35.0000	0	37.0000	2218.00

The data can be summarized as follows:

• \(n\) = 2290
• \(\pi_0\) = 1.3105%
• \(R_{11}\) = 35 (which is denoted as R1 in the package).
• \(\bar{R}_{11}\) = 33.3589 (which is denoted as R1 or R1w in the package).
• \(R_{10}\) = 0 (which is denoted as R2 in the package).
• \(\bar{R}_{10}\) = 0 (which is denoted as R2 or R2w in the package).
• \(R_{01}\) = 37 (which is denoted as R3 in the package).
• \(\bar{R}_{01}\) = 38.2712 (which is denoted as R3 or R3w in the package).
• \(R_{00}\) = 2218 (which is denoted as R4 in the package).
• \(\bar{R}_{00}\) = 2218.3698 (which is denoted as R4 or R4w in the package).

We can check that \(R_{11} + R_{10} + R_{01} + R_{00} = n\)

R1 + R2 + R3 + R4

## [1] 2290

and \(\bar{R}_{11} + \bar{R}_{10} + \bar{R}_{01} + \bar{R}_{00} = n\)

R1w + R2w + R3w + R4w

## [1] 2290

For the analysis we consider the possibility of measurement error, in which we use the following values:

# Measurement error
alpha0 = 0
alpha = 1/100
beta = 10/100

Survey MLE

Survey MLE with random sampling

The Survey MLE (with and without measurement error) can be compute as follows and correspond to the number report in Table 3 of Guerrier, Kuzmics, and Victoria-Feser (2024):

# Survey MLE without measurement error
(smle_no_meas_error_random = survey_mle(R = R1 + R3, n = n))

## Method: Survey MLE
## 
## Estimated proportion: 3.1441%
## Standard error      : 0.3647%
## 
## Confidence intervals at the 95% level:
## Asymptotic Approach: 2.4294% - 3.8588%
## Clopper-Pearson    : 2.4680% - 3.9433%
## 
## Assumed measurement error: alpha = 0%, beta = 0% 
## Sampling: Random

# Survey MLE with measurement error (as defined above)
(smle_with_meas_error_random = survey_mle(R = R1 + R3, n = n, 
                              alpha = alpha, beta = beta))

## Method: Survey MLE
## 
## Estimated proportion: 2.4091%
## Standard error      : 0.4097%
## 
## Confidence intervals at the 95% level:
## Asymptotic Approach: 1.6060% - 3.2122%
## Clopper-Pearson    : 1.6495% - 3.3070%
## 
## Assumed measurement error: alpha = 1%, beta = 10% 
## Sampling: Random

Survey MLE with stratified sampling

In the case of a stratified sampling, the Survey MLE (with and without measurement error) can be compute as follows:

# Survey (weighted) MLE without measurement error
(smle_no_meas_error_strat = survey_mle(R = R1w + R3w, n = n, 
                            V = mean(covid19_austria$weights^2)))

## Method: Survey MLE
## 
## Estimated proportion: 3.1280%
## Standard error      : 0.4471%
## 
## Confidence interval at the 95% level:
## Asymptotic Approach: 2.2517% - 4.0042%
## 
## Assumed measurement error: alpha = 0%, beta = 0% 
## Sampling: Stratified with V = 1.51

# Survey MLE with measurement error (as defined above)
(smle_with_meas_error_strat = survey_mle(R = R1w + R3w, n = n,
                             alpha = alpha, beta = beta, 
                             V = mean(covid19_austria$weights^2)))

## Method: Survey MLE
## 
## Estimated proportion: 2.3910%
## Standard error      : 0.5023%
## 
## Confidence interval at the 95% level:
## Asymptotic Approach: 1.4064% - 3.3755%
## 
## Assumed measurement error: alpha = 1%, beta = 10% 
## Sampling: Stratified with V = 1.51

Moment-based estimator

Moment-based estimator with random sampling

In the case of a random sampling, the moment-based estimator or MME (with and without measurement error) can be compute as follows:

# MME without measurement error
(mme_no_meas_error_random = moment_estimator(R3 = R3, n = n, 
                            pi0 = pi0))

## Method: Moment Estimator
## 
## Estimated proportion: 2.9262%
## Standard error      : 0.2635%
## 
## Confidence intervals at the 95% level:
## Asymptotic Approach: 2.4099% - 3.4426%
## Clopper-Pearson    : 2.4506% - 3.5308%
## 
## Assumed measurement error: alpha  = 0%, beta = 0%,
##                            alpha0 = 0% 
## 
## Estimated false negative rate of the
## official procedure: beta0 = 55.21%
## CI at the 95% level: 47.31% - 63.12%
## 
## Estimated ascertainment rate: 
## pi0/pi = 44.79%
## CI at the 95% level: 36.88% - 52.69%
## 
## Sampling: Random

# MME with measurement error (as defined above)
(mme_with_meas_error_random = moment_estimator(R3 = R3, n = n,
                              pi0 = pi0, alpha = alpha, 
                              beta = beta, alpha0 = alpha0))

## Method: Moment Estimator
## 
## Estimated proportion: 2.0171%
## Standard error      : 0.2960%
## 
## Confidence intervals at the 95% level:
## Asymptotic Approach: 1.4369% - 2.5973%
## Clopper-Pearson    : 1.4827% - 2.6963%
## 
## Assumed measurement error: alpha  = 1%, beta = 10%,
##                            alpha0 = 0% 
## 
## Estimated false negative rate of the
## official procedure: beta0 = 35.03%
## CI at the 95% level: 16.34% - 53.72%
## 
## Estimated ascertainment rate: 
## pi0/pi = 64.97%
## CI at the 95% level: 46.28% - 83.66%
## 
## Sampling: Random

Moment-based estimator with stratified sampling

In the case of a stratified sampling, the MME (with and without measurement error) can be compute as follows and correspond to the number report in Table 3 of Guerrier, Kuzmics, and Victoria-Feser (2024):

# MME without measurement error
(mme_no_meas_error_strat = moment_estimator(R3 = R3w, n = n,
                          pi0 = pi0,
                          V = mean(covid19_austria$weights^2)))

## Method: Moment Estimator
## 
## Estimated proportion: 2.9818%
## Standard error      : 0.3292%
## 
## Confidence interval at the 95% level:
## Asymptotic Approach: 2.3365% - 3.6270%
## 
## Assumed measurement error: alpha  = 0%, beta = 0%,
##                            alpha0 = 0% 
## 
## Estimated false negative rate of the
## official procedure: beta0 = 56.05%
## CI at the 95% level: 46.54% - 65.56%
## 
## Estimated ascertainment rate: 
## pi0/pi = 43.95%
## CI at the 95% level: 34.44% - 53.46%
## 
## Sampling: Stratified with V = 1.51

# MME with measurement error (as defined above)
(mme_with_meas_error_strat = moment_estimator(R3 = R3w, n = n,
                             pi0 = pi0, alpha = alpha, beta = beta,
                             alpha0 = alpha0, 
                             V = mean(covid19_austria$weights^2)))

## Method: Moment Estimator
## 
## Estimated proportion: 2.0794%
## Standard error      : 0.3699%
## 
## Confidence interval at the 95% level:
## Asymptotic Approach: 1.3544% - 2.8045%
## 
## Assumed measurement error: alpha  = 1%, beta = 10%,
##                            alpha0 = 0% 
## 
## Estimated false negative rate of the
## official procedure: beta0 = 36.98%
## CI at the 95% level: 15.00% - 58.95%
## 
## Estimated ascertainment rate: 
## pi0/pi = 63.02%
## CI at the 95% level: 41.05% - 85.00%
## 
## Sampling: Stratified with V = 1.51

Conditional MLE

Conditional MLE with random sampling

In the case of a random sampling, the conditional MLE or CMLE (with and without measurement error) can be compute as follows:

# CMLE without measurement error
(cmle_no_meas_error_random = conditional_mle(R1 = R1, R2 = R2, 
                            R3 = R3, R4 = R4, pi0 = pi0))

## Method: Conditional MLE
## 
## Estimated proportion: 2.9317%
## Standard error      : 0.2639%
## 
## Confidence interval at the 95% level:
## Asymptotic Approach: 2.4145% - 3.4489%
## 
## Assumed measurement error: alpha  = 0%, beta = 0%,
##                            alpha0 = 0% 
## 
## Estimated false negative rate of the
## official procedure: beta0 = 55.30%
## CI at the 95% level: 47.41% - 63.18%
## 
## Estimated ascertainment rate: 
## pi0/pi = 44.70%
## CI at the 95% level: 36.82% - 52.59%
## 
## Sampling: Random

# CMLE with measurement error (as defined above)
(cmle_with_meas_error_random = conditional_mle(R1 = R1, R2 = R2, 
                              R3 = R3, R4 = R4, pi0 = pi0, 
                              alpha = alpha, beta = beta, 
                              alpha0 = alpha0))

## Method: Conditional MLE
## 
## Estimated proportion: 2.0200%
## Standard error      : 0.2962%
## 
## Confidence interval at the 95% level:
## Asymptotic Approach: 1.4394% - 2.6006%
## 
## Assumed measurement error: alpha  = 1%, beta = 10%,
##                            alpha0 = 0% 
## 
## Estimated false negative rate of the
## official procedure: beta0 = 35.12%
## CI at the 95% level: 16.48% - 53.77%
## 
## Estimated ascertainment rate: 
## pi0/pi = 64.88%
## CI at the 95% level: 46.23% - 83.52%
## 
## Sampling: Random

Conditional MLE with stratified sampling

In the case of a stratified sampling, the CMLE (with and without measurement error) can be compute as follows:

# CMLE without measurement error
(cmle_no_meas_error_strat = conditional_mle(R1 = R1w, R2 = R2w, 
                            R3 = R3w, R4 = R4w, pi0 = pi0, 
                            V = mean(covid19_austria$weights^2)))

## Method: Conditional MLE
## 
## Estimated proportion: 2.9841%
## Standard error      : 0.3294%
## 
## Confidence interval at the 95% level:
## Asymptotic Approach: 2.3385% - 3.6297%
## 
## Assumed measurement error: alpha  = 0%, beta = 0%,
##                            alpha0 = 0% 
## 
## Estimated false negative rate of the
## official procedure: beta0 = 56.08%
## CI at the 95% level: 46.58% - 65.59%
## 
## Estimated ascertainment rate: 
## pi0/pi = 43.92%
## CI at the 95% level: 34.41% - 53.42%
## 
## Sampling: Stratified with V = 1.51

# CMLE with measurement error (as defined above)
(cmle_with_meas_error_strat = conditional_mle(R1 = R1w, R2 = R2w, 
                              R3 = R3w, R4 = R4w, n = n, pi0 = pi0,
                              alpha = alpha, beta = beta, 
                              alpha0 = alpha0, 
                              V = mean(covid19_austria$weights^2)))

## Method: Conditional MLE
## 
## Estimated proportion: 2.0831%
## Standard error      : 0.3702%
## 
## Confidence interval at the 95% level:
## Asymptotic Approach: 1.3574% - 2.8087%
## 
## Assumed measurement error: alpha  = 1%, beta = 10%,
##                            alpha0 = 0% 
## 
## Estimated false negative rate of the
## official procedure: beta0 = 37.09%
## CI at the 95% level: 15.17% - 59.00%
## 
## Estimated ascertainment rate: 
## pi0/pi = 62.91%
## CI at the 95% level: 41.00% - 84.83%
## 
## Sampling: Stratified with V = 1.51

Marginal MLE

Marginal MLE with random sampling

In the case of a random sampling, the marginal MLE or MMLE (with and without measurement error) can be compute as follows:

# MMLE without measurement error
(mmle_no_meas_error_random = marginal_mle(R1 = R1, R3 = R3, n = n, pi0 = pi0))

## Method: Marginal MLE
## 
## Estimated proportion: 2.9317%
## Standard error      : 0.2639%
## 
## Confidence interval at the 95% level:
## Asymptotic Approach: 2.4145% - 3.4489%
## 
## Assumed measurement error: alpha  = 0%, beta = 0%,
##                            alpha0 = 0% 
## 
## Estimated false negative rate of the
## official procedure: beta0 = 55.30%
## CI at the 95% level: 47.41% - 63.18%
## 
## Estimated ascertainment rate: 
## pi0/pi = 44.70%
## CI at the 95% level: 36.82% - 52.59%
## 
## Sampling: Random

# MMLE with measurement error (as defined above)
(mmle_with_meas_error_random  = marginal_mle(R1 = R1, R3 = R3, n = n, pi0 = pi0, alpha = alpha, beta = beta, alpha0 = alpha0))

## Method: Marginal MLE
## 
## Estimated proportion: 2.0200%
## Standard error      : 0.2962%
## 
## Confidence interval at the 95% level:
## Asymptotic Approach: 1.4394% - 2.6006%
## 
## Assumed measurement error: alpha  = 1%, beta = 10%,
##                            alpha0 = 0% 
## 
## Estimated false negative rate of the
## official procedure: beta0 = 35.12%
## CI at the 95% level: 16.48% - 53.77%
## 
## Estimated ascertainment rate: 
## pi0/pi = 64.88%
## CI at the 95% level: 46.23% - 83.52%
## 
## Sampling: Random

Marginal MLE with stratified sampling

The MMLE is currently not implemented in the case of a stratified sampling.

Replicating Table 3

Table 3 can be replicated as follows:

table2 = matrix(NA, 6, 6)
rownames(table2) = c("SMLE (stratified)", "MME (stratified)", "Estimated beta0 (stratified)", "SMLE (random)", "MME (random)", "Estimated beta0 (random)")
colnames(table2) = c("Estimates (no meas. err.)", "95% CI (low)", "95% CI (high)", "Estimates (with meas. err.)", "95% CI (low)", "95% CI (high)")

table2[1, ] = 100*c(smle_no_meas_error_strat$estimate,
                smle_no_meas_error_strat$ci_asym,
                smle_with_meas_error_strat$estimate,
                smle_with_meas_error_strat$ci_asym) 

table2[2, ] = 100*c(mme_no_meas_error_strat$estimate,
                mme_no_meas_error_strat$ci_asym,
                mme_with_meas_error_strat$estimate,
                mme_with_meas_error_strat$ci_asym) 

table2[3, ] = 100*c(mme_no_meas_error_strat$beta0,
                mme_no_meas_error_strat$ci_beta0,
                mme_with_meas_error_strat$beta0,
                mme_with_meas_error_strat$ci_beta0)

table2[4, ] = 100*c(smle_no_meas_error_random$estimate,
                smle_no_meas_error_random$ci_asym,
                smle_with_meas_error_random$estimate,
                smle_with_meas_error_random$ci_asym)

table2[5, ] = 100*c(mme_no_meas_error_random$estimate,
                mme_no_meas_error_random$ci_asym,
                mme_with_meas_error_random$estimate,
                mme_with_meas_error_random$ci_asym) 
table2[6, ] = 100*c(mme_no_meas_error_random$beta0,
                mme_no_meas_error_random$ci_beta0,
                mme_with_meas_error_random$beta0,
                mme_with_meas_error_random$ci_beta0)

knitr::kable(round(table2, 3))

	Estimates (no meas. err.)	95% CI (low)	95% CI (high)	Estimates (with meas. err.)	95% CI (low)	95% CI (high)
SMLE (stratified)	3.128	2.252	4.004	2.391	1.406	3.375
MME (stratified)	2.982	2.336	3.627	2.079	1.354	2.804
Estimated beta0 (stratified)	56.049	46.537	65.560	36.977	15.003	58.951
SMLE (random)	3.144	2.429	3.859	2.409	1.606	3.212
MME (random)	2.926	2.410	3.443	2.017	1.437	2.597
Estimated beta0 (random)	55.215	47.312	63.118	35.028	16.339	53.718

Comparing prevalence

This figure can be obtained by running the file pempi/figures/case_study.Rnw. A similar base R version can be obtained as follows:

pi0 = 93914/7166167
cols = c("#F8766DFF", "#00BFC4FF")
delta = 0.1
cex_pt = 1.5
lwd_ci = 2
pch_mme = 16
pch_smle = 15

plot(NA, xlim = c(0.75, 4.25), ylim = c(1, 4), axes = FALSE, ann = FALSE)
grid()
box()
col_text = "grey60"
cex_text = 0.85
cex_text2 = 0.65
abline(v = c(1.5, 2.5, 3.5), col = col_text)

axis(2)

mtext("Stratified sampling", side = 3, line = 1.75, cex = cex_text, at = 1, col = col_text)
mtext("no measurment error", side = 3, line = 0.75, cex = cex_text2, at = 1, col = col_text)

mtext("Random sampling", side = 3, line = 1.75, cex = cex_text, at = 2, col = col_text)
mtext("no measurment error", side = 3, line = 0.75, cex = cex_text2, at = 2, col = col_text)

mtext("Stratified sampling", side = 3, line = 1.75, cex = cex_text, at = 3, col = col_text)
mtext("with measurment error", side = 3, line = 0.75, cex = cex_text2, at = 3, col = col_text)

mtext("Random sampling", side = 3, line = 1.75, cex = cex_text, at = 4, col = col_text)
mtext("with measurment error", side = 3, line = 0.75, cex = cex_text2, at = 4, col = col_text)

mtext("Prevalence (%)", side = 2, line = 3, cex = 1.15)
abline(h = 100*pi0, lwd = 2, lty = 2)

text(1, 1.18, expression(pi[0]), cex = 1.15)

legend("topright", c("MME", "95% CI",
                    "Survey MLE", "95% CI"),
       bty = "n", col = c(cols[1], cols[1], cols[2], cols[2]),
       lwd = c(NA, lwd_ci, NA, lwd_ci), pch = c(pch_mme, NA, pch_smle, NA),
       pt.cex = 1.5, cex = 0.7)

# 1) Stratified sampling, without ME
points(1 - delta, 100*mme_no_meas_error_strat$estimate, col = cols[1], pch = pch_mme, cex = cex_pt)
lines(c(1, 1) - delta, 100*mme_no_meas_error_strat$ci_asym, col = cols[1], lwd = lwd_ci)

points(1 + delta, 100*smle_no_meas_error_strat$estimate, col = cols[2], pch = pch_smle, cex = cex_pt)
lines(c(1, 1) + delta, 100*smle_no_meas_error_strat$ci_asym, col = cols[2], lwd = lwd_ci)

# 2) Random sampling, without ME
points(2 - delta, 100*mme_no_meas_error_random$estimate, col = cols[1], pch = pch_mme, cex = cex_pt)
lines(c(2, 2) - delta, 100*mme_no_meas_error_random$ci_asym, col = cols[1], lwd = lwd_ci)

points(2 + delta, 100*smle_no_meas_error_random$estimate, col = cols[2], pch = pch_smle, cex = cex_pt)
lines(c(2, 2) + delta, 100*smle_no_meas_error_random$ci_asym, col = cols[2], lwd = lwd_ci)

# 3) Stratified sampling, with ME
points(3 - delta, 100*mme_with_meas_error_strat$estimate, col = cols[1], pch = pch_mme, cex = cex_pt)
lines(c(3, 3) - delta, 100*mme_with_meas_error_strat$ci_asym, col = cols[1], lwd = lwd_ci)

points(3 + delta, 100*smle_with_meas_error_strat$estimate, col = cols[2], pch = pch_smle, cex = cex_pt)
lines(c(3, 3) + delta, 100*smle_with_meas_error_strat$ci_asym, col = cols[2], lwd = lwd_ci)

# 4) Random sampling, with ME
points(4 - delta, 100*mme_with_meas_error_random$estimate, col = cols[1], pch = pch_mme, cex = cex_pt)
lines(c(4, 4) - delta, 100*mme_with_meas_error_random$ci_asym, col = cols[1], lwd = lwd_ci)

points(4 + delta, 100*smle_with_meas_error_random$estimate, col = cols[2], pch = pch_smle, cex = cex_pt)
lines(c(4, 4) + delta, 100*smle_with_meas_error_random$ci_asym, col = cols[2], lwd = lwd_ci)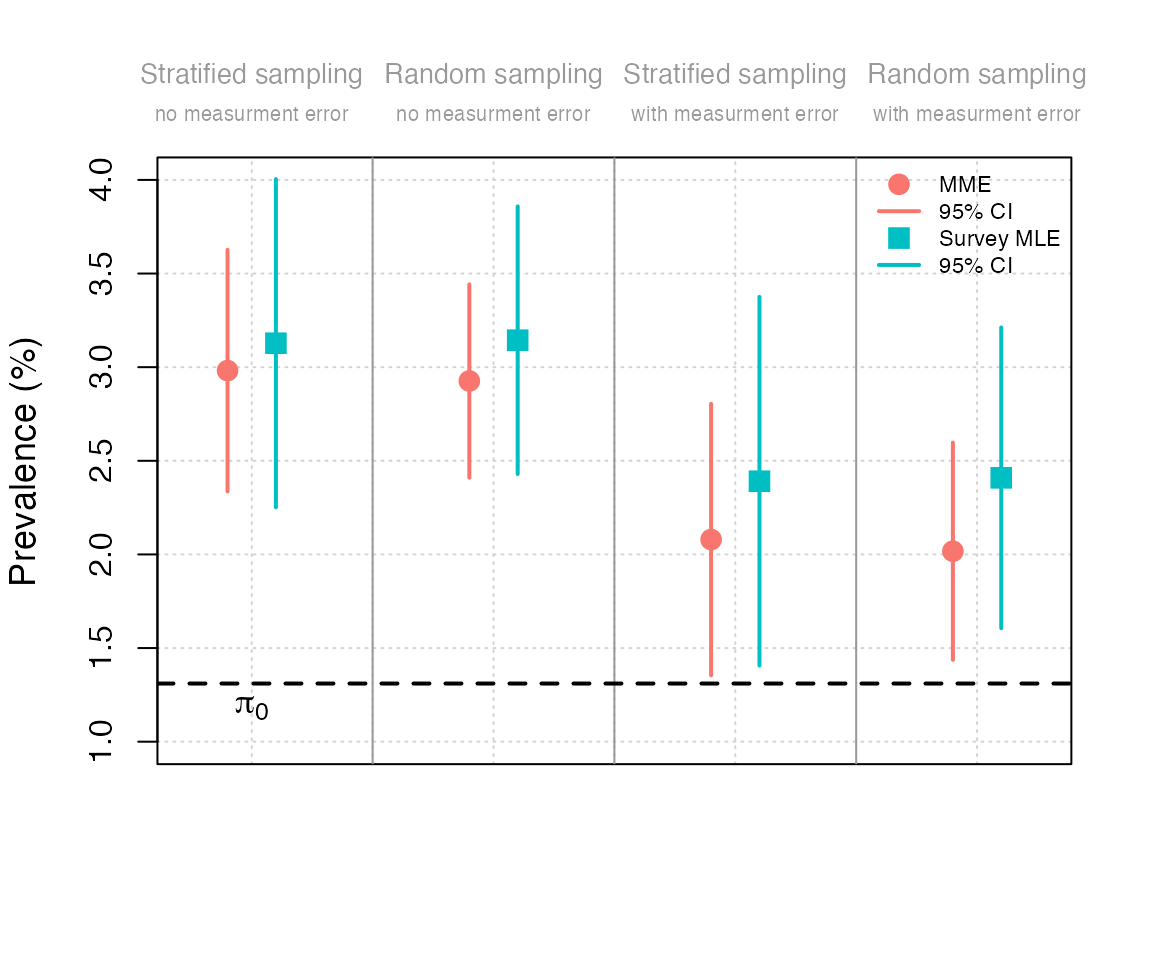

Replicating Figure 1

Figure 1 can be obtained by running the file pempi/figures/case_study.Rnw. A similar base R version can be obtained as follows:

# Assumptions
pi0 = 93914/7166167
alpha = 1/100
alpha0 = 0
m = 300
beta = seq(from = 0, to = 30, length.out = m)/100
res_moment = res_smle = matrix(NA, m, 3)
V = mean(covid19_austria$weights^2)

for (i in 1:m){
  # Moment estimator
  inter = moment_estimator(R3 = R3w, n = n, pi0 = pi0,
                           alpha = alpha, alpha0 = alpha0,
                           beta = beta[i], V = V)

  res_moment[i,] = c(inter$estimate, inter$ci_asym)

  # Survey MLE
  inter = survey_mle(R = R1w + R3w, n = n, pi0 = pi0,
                     alpha = alpha, alpha0 = alpha0,
                     beta = beta[i], V = V)

  res_smle[i,] = c(inter$estimate, inter$ci_asym)
}

cols = c("#F8766DFF", "#00BFC4FF")
cols2 = c("#F8766D1F", "#00BFC41F")

plot(NA, xlim = 100*range(beta), ylim = c(1, 4.25), axes = FALSE, ann = FALSE)
grid()
box()
axis(1)
axis(2)
mtext(expression(paste(beta, " (%)")), side = 1, line = 3, cex = 1.15)
mtext("Prevalence (%)", side = 2, line = 3, cex = 1.15)
abline(h = 100*pi0, lwd = 2, lty = 2)
abline(h = 100*pi0, lwd = 2, lty = 2)

text(2.5, 1.18, expression(pi[0]), cex = 1.15)

legend("topleft", c("MME", "95% CI",
                    "Survey MLE", "95% CI"),
       bty = "n", col = c(cols[1], cols2[1],cols[2], cols2[2]),
       lwd = c(3, NA, 3, NA), pch = c(NA, 15, NA, 15),
       pt.cex = 2.5)
lines(100*beta, 100*res_moment[,1], lwd = 3, col = cols[1])
polygon(100*c(beta, rev(beta)),
        100*c(res_moment[,2], rev(res_moment[,3])),
        col = cols2[1], border = NA)

lines(100*beta, 100*res_smle[,1], lwd = 3, col = cols[2])
polygon(100*c(beta, rev(beta)),
        100*c(res_smle[,2], rev(res_smle[,3])),
        col = cols2[2], border = NA)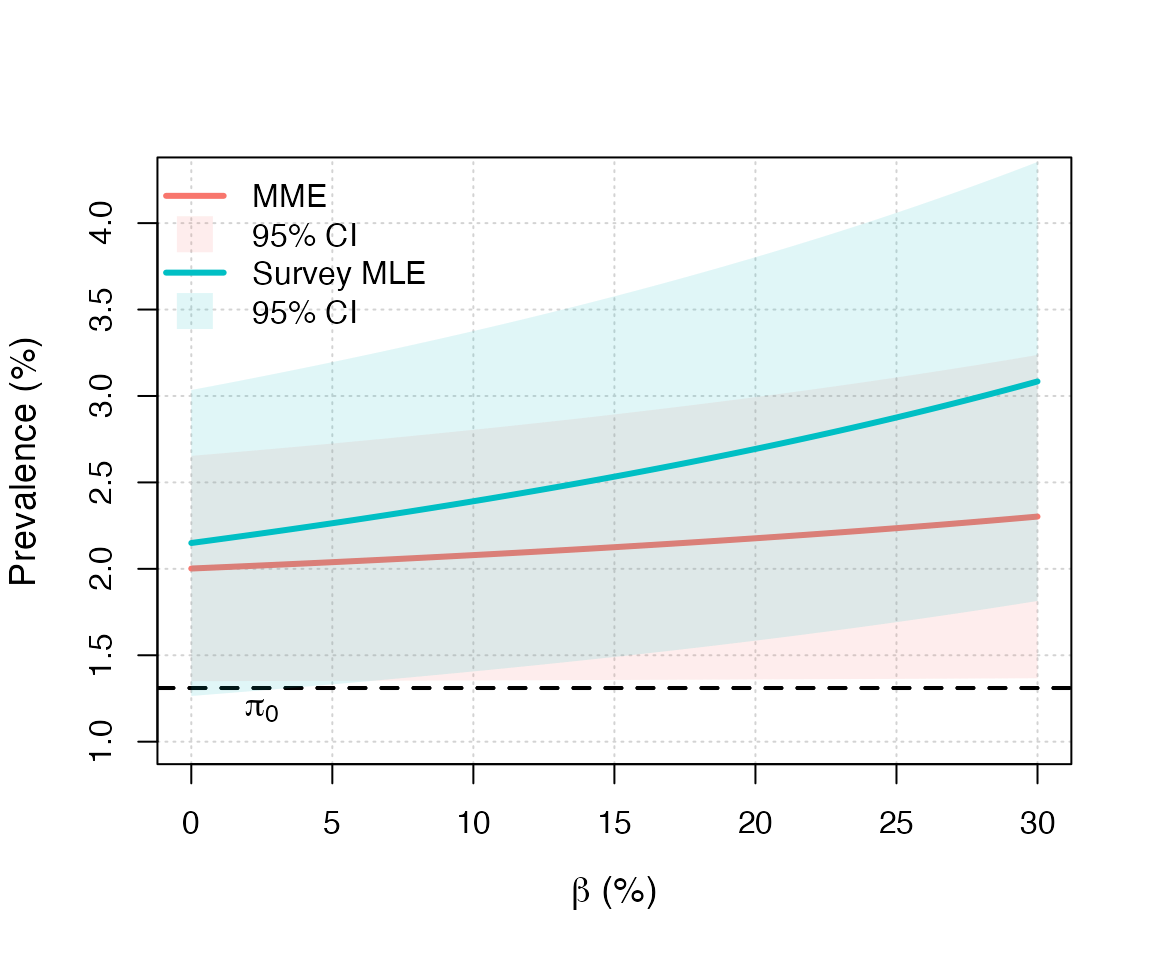

Simulation Study

The results summarized in Section 5 Guerrier, Kuzmics, and Victoria-Feser (2024) can be replicated as follows:

1. Run the file pempi/simulations/simulation_script.R which should take a couple of hours on a standard laptop (with \(5 \times 10^4\) Monte Carlo replications). This allows to generate the file pempi/simulations/simulations.RData.
2. Run the file pempi/simulations/figures.Rnw (which reads pempi/simulations/simulations.RData) to generate the figures associated to our simulation study.

References

Guerrier, Stéphane, Christoph Kuzmics, and Maria-Pia Victoria-Feser. 2024. “Assessing COVID-19 Prevalence in Austria with Infection Surveys and Case Count Data as Auxiliary Information.” Journal of the American Statistical Association, in Press.

Statistics Austria. 2020. “Prävalenz von SARS-CoV-2-Infektionen liegt bei 3,1%.”